Chord names/diagrams

Here’s how to work with chord names and diagrams using the Soundslice editor.

Entering chords

1. Select the note or rest above which you’d like to add a chord.
2. In the editor’s top panel, open the “Text” section and click the “Chord name/diagram” button . Or search the editor for “Chord name” or use a keyboard shortcut.
3. At the left of your screen, you’ll see a place for you to enter the chord.

Editing chords

To edit an existing chord, just click on it. The chord-entry interface will appear at left, and you can make changes.

Chord diagrams

If your instrument has tablature enabled, your chords can optionally include chord diagrams. These diagrams will always use the same number of strings as in your tablature.

If you create a chord above a beat that has at least three notes already entered, we’ll automatically pull those notes into the chord diagram when you open the chord-entry interface. You can change the auto-generated diagram by typing in or removing the fret numbers that appear beneath the chord name.

You can also just add the chord name and type in the frets manually:

Fret numbers in chord diagrams

For chords that are played up the neck, we automatically determine which fret number to display on the left. It’s the fret number of the lowest fretted string in the chord. For example, here it’s 8:

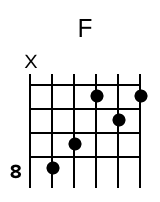
At the moment, there’s no way to change this.

Chord positions

After you enter a chord, it’s “locked” to that rhythmic position. (An example rhythmic position is “a quarter note’s duration from the start of the bar.”)

So if you enter a chord, then delete or move the note below it, the chord will remain in place. This makes it possible to create notation like this, in which chords are “floating” above empty space:

To accomplish this, follow these steps:

1. Enter some notes/rests at the rhythmic positions that will hold those chords.
2. Add the chords.
3. Delete the notes/rests. The chords will remain in position.

Can I use the ‘text above’ feature to add chord names?

You can, but we don’t recommend it. If you use the proper “chord” feature as opposed to “text,” then Soundslice will automatically give you some cool features. Anybody viewing your slice will be able to:

• Transpose chords
• Hide the chord names/diagrams
• Toggle between “show names/diagrams,” “show only names” and “hide names/diagrams”
• Enable chord-chart view
• Likely new amazing features in the future!

Put simply: If Soundslice knows that a given piece of information is a chord, it can do more interesting things.

Can I mix and match chords-with-diagrams and chords-without-diagrams within a single instrument?

Yes, no problem.

Can I use a chord diagram in an instrument that doesn’t have tablature?

Not at this time, because the system wouldn’t know how many strings to use in the diagram.

How can I use sharp or flat symbols in chord names?

Use the lowercase B and pound signs symbols when entering the chord name. Our system will automatically convert the following:

• b (lowercase B) will be converted to ♭ (flat symbol)
• # (pound sign) will be converted to ♯ (sharp symbol)
• bb (two lowercase Bs) will be converted to 𝄫 (double-flat symbol)
• ## (two pound signs) will be converted to 𝄪 (double-sharp symbol)

For example, to write the chord B♭ (B flat), write “Bb” (a capital B followed by a lowercase B).

As convention is to simply omit natural symbols in chord names, so we don’t have a shortcut for the natural symbol.

Can I change the font used in chord names?

Not at this time. This is on our to-do list.

Can I use fancy superscript/subscript stuff in chord names?

Not at this time. This is on our to-do list.

Is it possible to add alternate chords above the primary chord names?

Not at this time. We only support a single chord name at a given rhythmic location.

If you’d like to display alternatives, we’d recommend using inner or outer text as a workaround (despite what we wrote above about the limitations of this technique).